hottriada.blogg.se

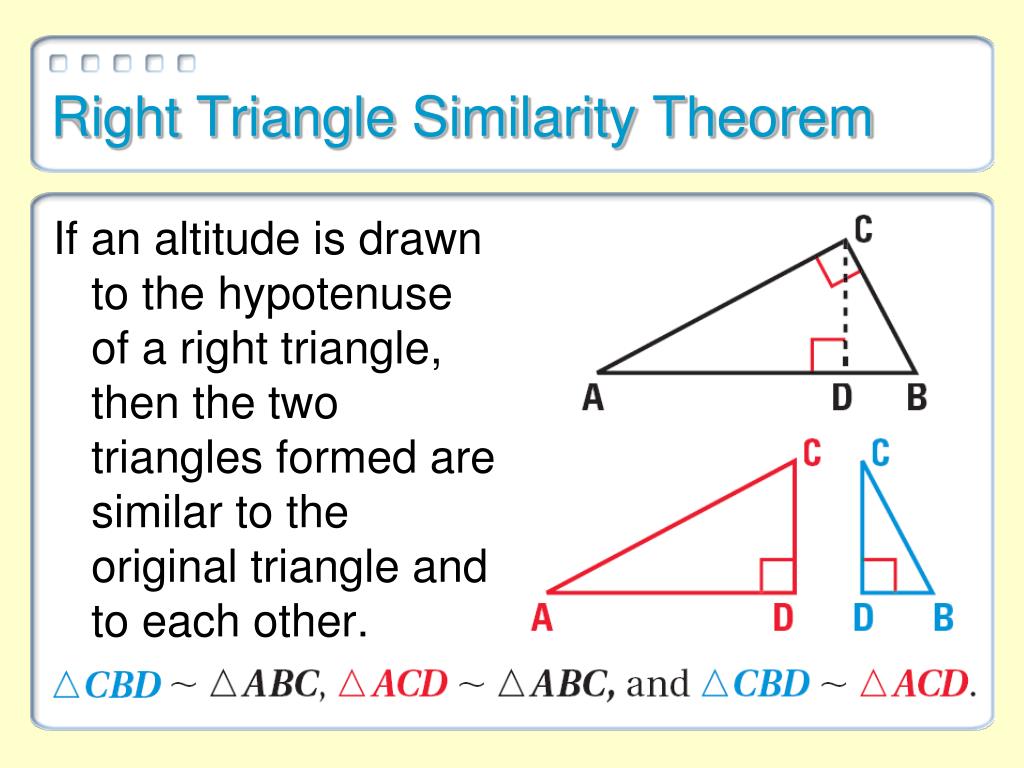
This is Theorem 9-2 FGH is a right triangle with right FGH and the altitude of the hypotenuse. In a right-angled triangle, we only need to know one other angle and then the angle sum of a triangle gives us the third angle. Similarity in Right Triangles Theorem 9.2 Key Concepts/Examples: If you draw an altitude from the right angle to the hypotenuse of a right triangle, you create three similar triangles. That is, once the angles of a triangle are fixed, the ratios of the sides of the triangle are constant. Hence the matching angles are the same.įor any right-angled triangle similar to triangle ABC, the ratio of the matching sides will be the same. The triangles pictured are similar (SSS), that is the corresponding sides are in the same ratio. This investigation is a great demonstration to help students visualize similar right triangles To begin, start with a regular sheet of paper. Source: Australian Curriculum, Assessment and Reporting Authority (ACARA) Similarity of right-angled triangles 3 : 4 is then the reduced form of the comparison of the perimeters.Use similarity to investigate the constancy of the sine, cosine and tangent ratios for a given angle in right-angled triangles (ACMMG223) Find the perimeter of each triangle.Ĭall the two triangles Δ 1 and Δ 2 and let the scale factor of the two similar triangles be a : b.Ī : b is the reduced form of the scale factor. If you call the triangles Δ 1 and Δ 2, thenĪccording to Theorem 60, this also means that the scale factor of these two similar triangles is 3 : 4.īecause the sum of the areas is 75 cm 2, you getĮxample 4: The areas of two similar triangles are 45 cm 2 and 80 cm 2. The scale factor of these similar triangles is 5 : 8.Įxample 3: The perimeters of two similar triangles is in the ratio 3 : 4. Find the area of Δ STU.įigure 4 Using the scale factor to determine the relationship between the areas of similar triangles. Theorem 61: If two similar triangles have a scale factor of a : b, then the ratio of their areas is a 2 : b 2.Įxample 2: In Figure 4, Δ PQR∼ Δ STU. If the altitude is drawn from the right angle of a right triangle to the hypotenuse, then the two right triangles formed are similar to the given right triangle. Now you can compare the ratio of the areas of these similar triangles. You can now find the area of each triangle.įigure 3 Finding the areas of similar right triangles whose scale factor is 2 : 3. Because GH ⊥ GI and JK ⊥ JL , they can be considered base and height for each triangle. Find the perimeter of Δ DEFįigure 3 shows two similar right triangles whose scale factor is 2 : 3. Theorem 60: If two similar triangles have a scale factor of a : b, then the ratio of their perimeters is a : b.Įxample 1: In Figure 2, Δ ABC∼ Δ DEF. When you compare the ratios of the perimeters of these similar triangles, you also get 2 : 1. The perimeter of Δ ABC is 24 inches, and the perimeter of Δ DEF is 12 inches. It is then said that the scale factor of these two similar triangles is 2 : 1. The ratios of corresponding sides are 6/3, 8/4, 10/5.

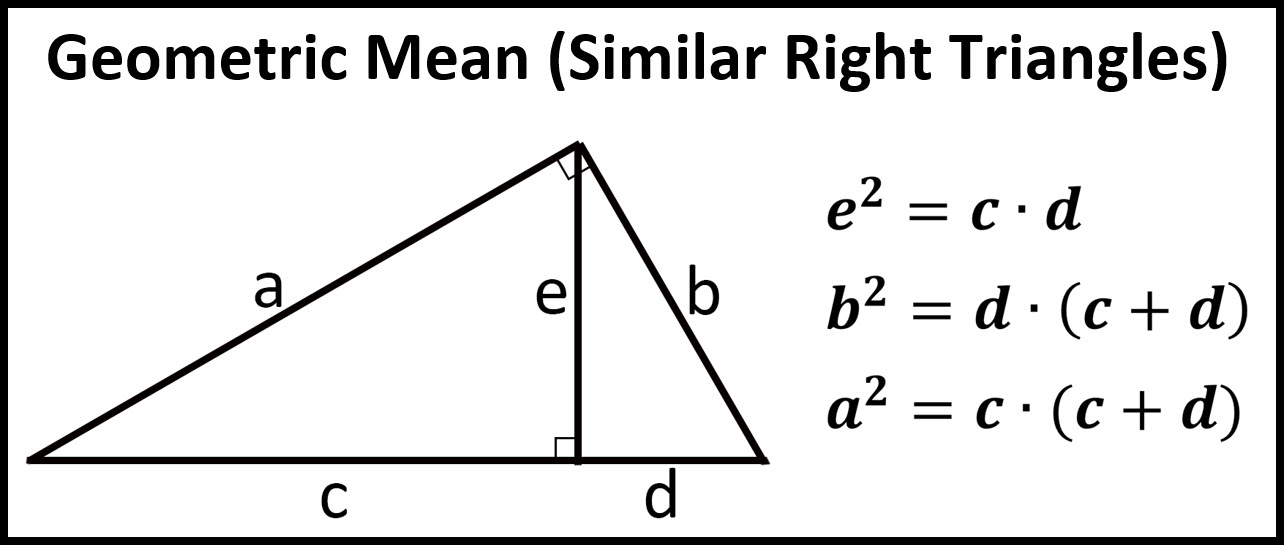
In Figure 1, Δ ABC∼ Δ DEF.įigure 1 Similar triangles whose scale factor is 2 : 1. A Pythagorean triple is a group of three whole Numbers that satisfies the equation a2+b2c2 where c is the greatest number. When two triangles are similar, the reduced ratio of any two corresponding sides is called the scale factor of the similar triangles. Solve for x and y y x2(8)(5) X6.3 y2(13)(8) y10.2 4.

Summary of Coordinate Geometry Formulas.Slopes: Parallel and Perpendicular Lines.

Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Use trigonometric ratios and the Pythagorean Theorem to solve right triangles in. Explain and use the relationship between the sine and cosine of complementary angles. Proving that Figures Are Parallelograms Understand that by similarity, side ratios in right triangles are properties of the angles in the triangle, leading to definitions of trigonometric ratios for acute angles.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.Classifying Triangles by Sides or Angles.Apply similarity relationships in right triangles to solve problems. Lines: Intersecting, Perpendicular, Parallel Use geometric mean to find segment lengths in right triangles.